type
status
date
slug
summary
category
tags
icon
password
随着七年级系统性开始学习几何,很多家长都会问我:这几何该咋学,孩子拿到题一点思路都没有,题目都看不懂,怎么办呢?
赵老师:这是没掌握方法,今天我就来聊聊,几何中的一套通用的方法:标记法+拆解法。
👉 标记法,帮助孩子读懂题干,搞清楚“说了什么”;
👉 拆解法,帮助孩子理清思路,知道“怎么下手”。
🧩 为什么代数学得好,几何却突然“哑火”?
进入七年级下学期,同学们都要系统地学习几何。很多原本在代数部分表现非常优秀的学生,在几何部分中突然“哑火”了。不是他们不努力,而是完全不适应几何题目的思维方式。这种落差,会让很多孩子产生挫败感,“为什么以前觉得数学很简单,现在却看不懂题?”、“这些辅助线是从哪里变出来的?”、“几何是不是就是靠天赋?”
我想分享一个学生的例子。他在七年级上学期的代数考试中基本都能拿满分,但到了下学期接触几何后,第一次见面他就对我说:“老师,我最讨厌的就是几何,完全不知道怎么分析,也不知道这些天马行空的辅助线到底是怎么做出来的。”
其实,这并不是他一个人的困惑,而是很多七年级学生都会遇到的普遍问题。
🧠 代数靠“计算”,几何靠“分析”
代数的学习更像是“算得快、步骤熟”,而几何是一种图形+语言+逻辑结合的“分析型”思维。
几何题并不是难在知识点,而是难在“看图分析”的这个过程:
- 信息看不全
- 条件理不清
- 辅助线不会画
- 推理链不完整
几何难学,并不是题难,而是思维没转弯。
几何背后的“逻辑拆解”和“图形分析”的思维模式。这套模式是全新的,需要系统训练和刻意练习才能建立。
那么,几何到底该怎么学?
📌 解题的底层逻辑:三步拆解法
下边讲的三步拆解法,是一个“容易学会”并且是“可复制”的思维流程:
✅ 第一步:慢读题干,翻译题目,标注“已知条件”
拿到一道几何题,不要急着找思路,而是要慢读题目,翻译题目,把题干读清楚,尤其要关注每一个“已知信息”。
同学自己也会直观的发现,题目中有一些显性条件的信息,就是题干中明确写出来告诉的条件,那些边相等,哪些边平行,哪些角相等,哪些角是倍数关系,哪两个三角形全等等等。把题干中的这些“已知信息”用几何的“标注语言”在几何图形中标注清晰。
很多学生不喜欢动手标图,喜欢用瞪眼大法,一切分析都在脑中运行,结果就是脑子里“混着想”,导致信息混乱、推导出错。
注意,用黑笔把这些信息清晰地标注在图形中,比如“∠ABC=90°”、“AB=AC”……这些条件是解题的基础,必须一眼可见、逻辑清晰。
标图,不是“可选动作”,而是进入几何的必修课。
👇 标注的时候要适当掌握一些标注的方法,以下是我带学生的时候会教会孩子的标注方法:
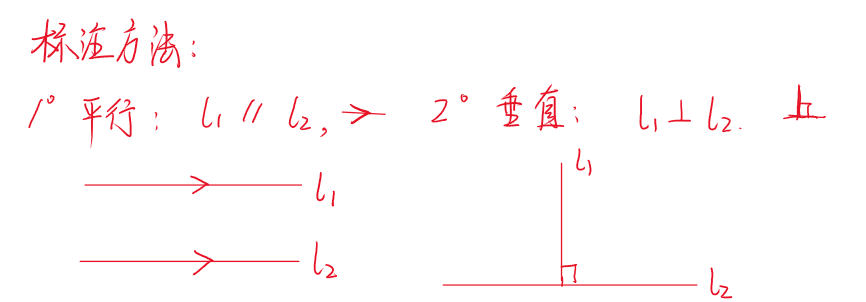
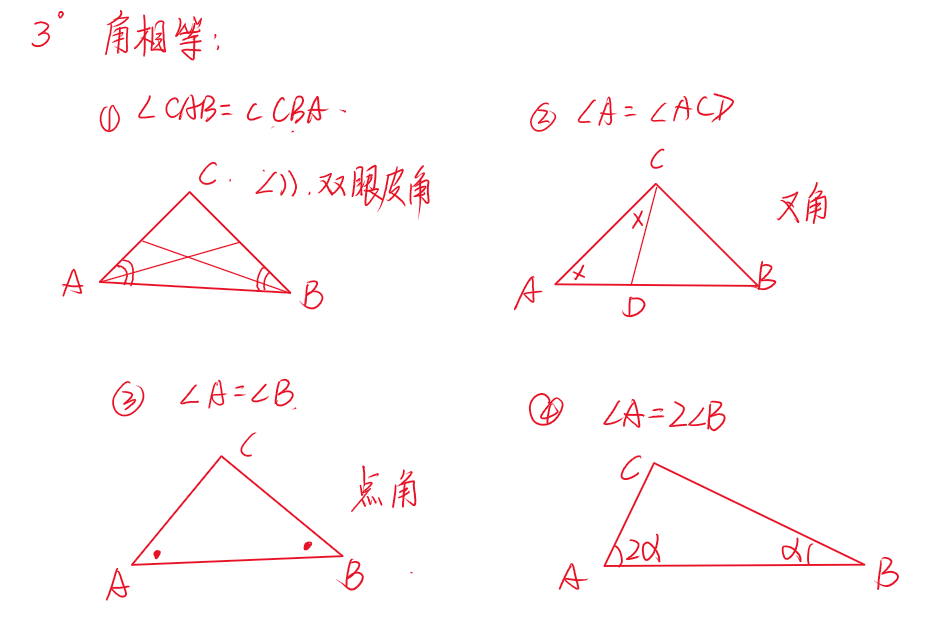
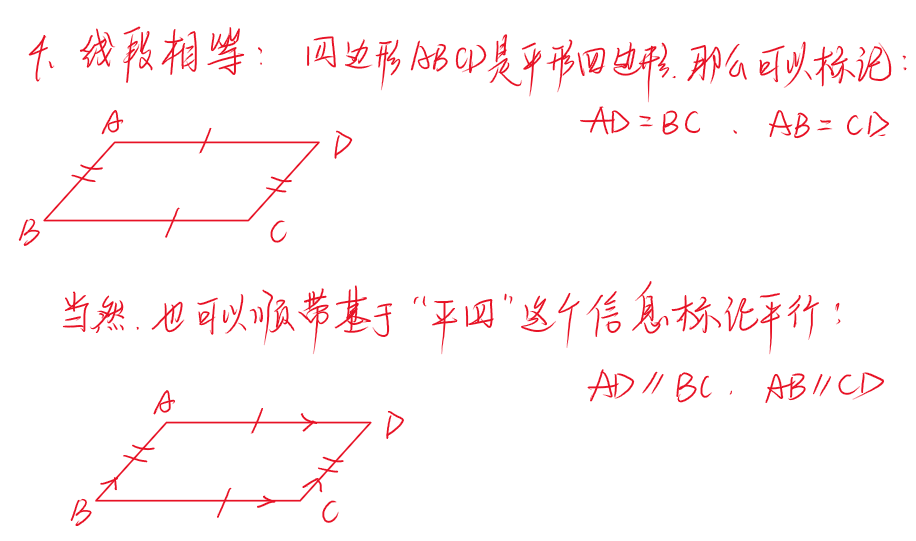
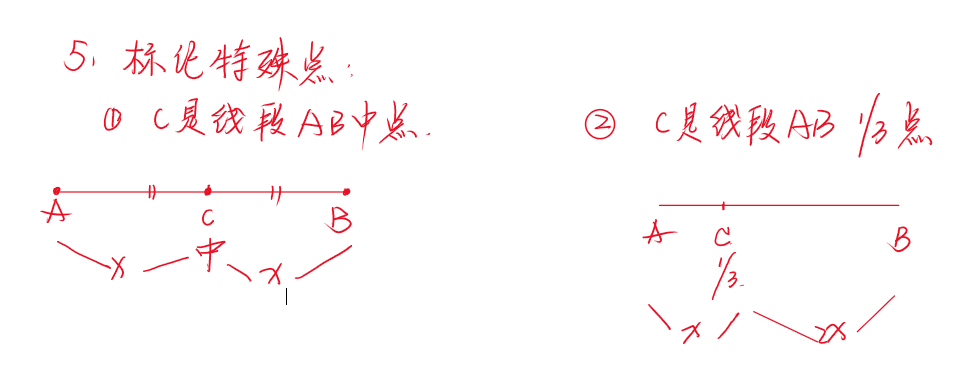
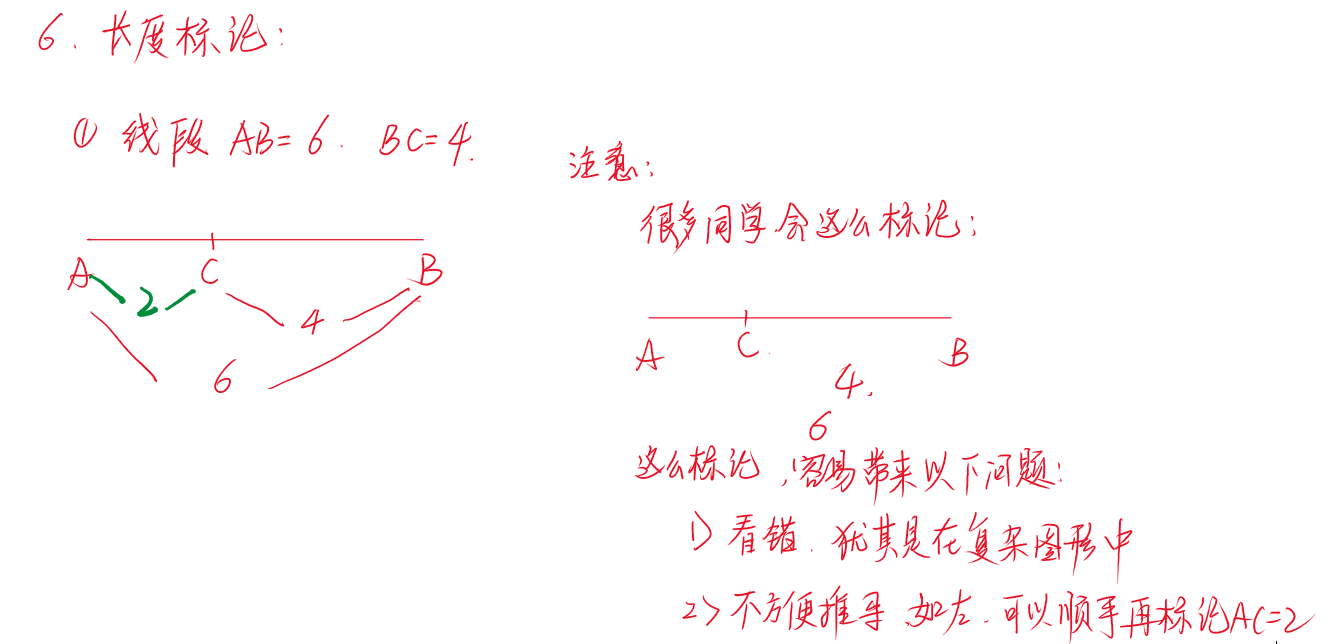
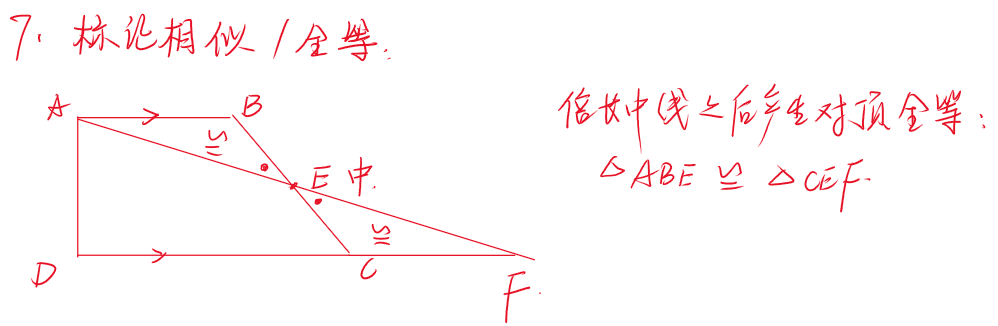
通过以上的标记之后,我们就可以把题目中的文字语言转换成几何图形的中的标记语言,如下:
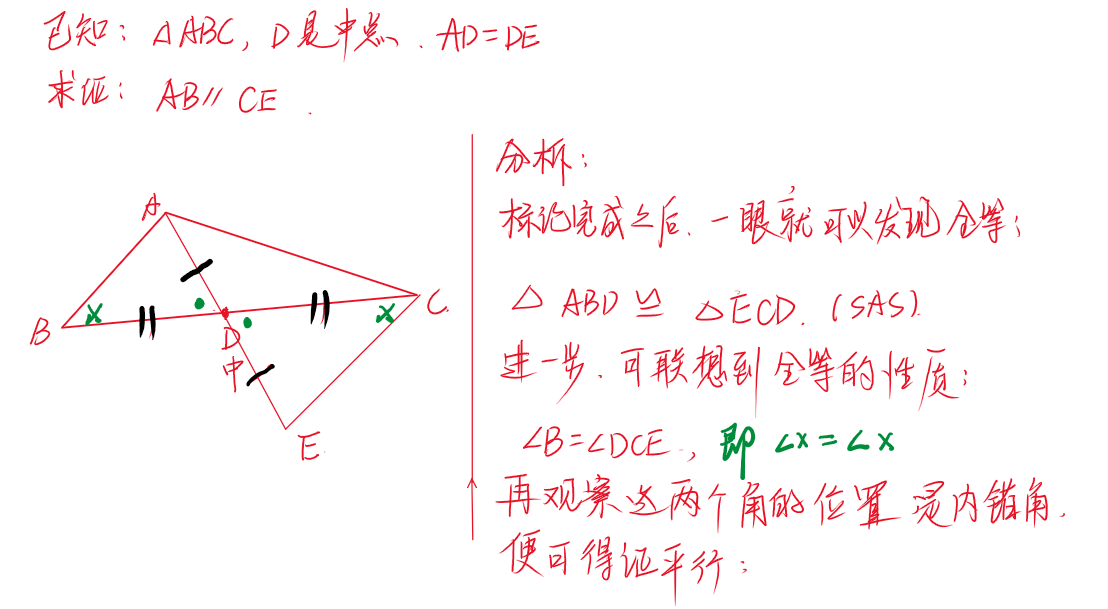

✅ 第二步:基于已知信息,继续“发散推导”,寻找隐性信息
显性信息标好之后,我们开始加工信息,通过已知条件,推论出很多隐藏条件。
接下来,用铅笔(区别于黑笔)在图中标出你通过思考推导出的角度、边长等新关系。这一步叫“信息再加工”。比如上边例题中用绿色笔和黑色比进行区分。
分析的过程中,比如,比如,题目只告诉你两条边相等。你要知道这是等腰三角形,要知道底角相等,要知道底边的三线合一,三线合一是哪三条线,有什么性质特征?……这些都是隐藏条件,都是通过已有条件推论出来的。
这个过程的核心是发散思维:一个条件和另一个条件能不能碰撞出新的信息?新信息是否能和其他条件继续结合?推导链条越长,说明你对题目的理解越深。
刚开始,很多学生完成这个阶段可能要五六分钟。但随着练习的深入,熟练之后两三分钟就足够了。
✅ 第三步:梳理信息,正推 or 反推求解
信息收集完毕,接下来就进入“解题环节”。要想解决问题,就要开始收敛,对多条思路快速试错,确定解题方向。这一步可以选择两种思路:
- 正推思维:从已知出发,一步步推理,直到推出题目要求你证明或计算的结论;
- 反推思维:从题目的“目标结论”倒过来思考——这个结论成立需要哪些条件?这些条件是否已经在你前面推导的信息中出现?
对于初学几何的学生来说,很多题目是先反推,后正推:目标定下来,再看看手里的“材料”够不够。
这种梳理信息和思路的过程非常重要,非常重要,非常重要,特别是针对一些压轴题的分析,有了这个过程,可以事半功倍。
我在课堂上经常会使用拆解的方法,先拆解分析思路,再书写证明过程。同学们自己做题目的时候也要模仿这个过程,直到把这个方法内化为自己的方法。
举一个例子:
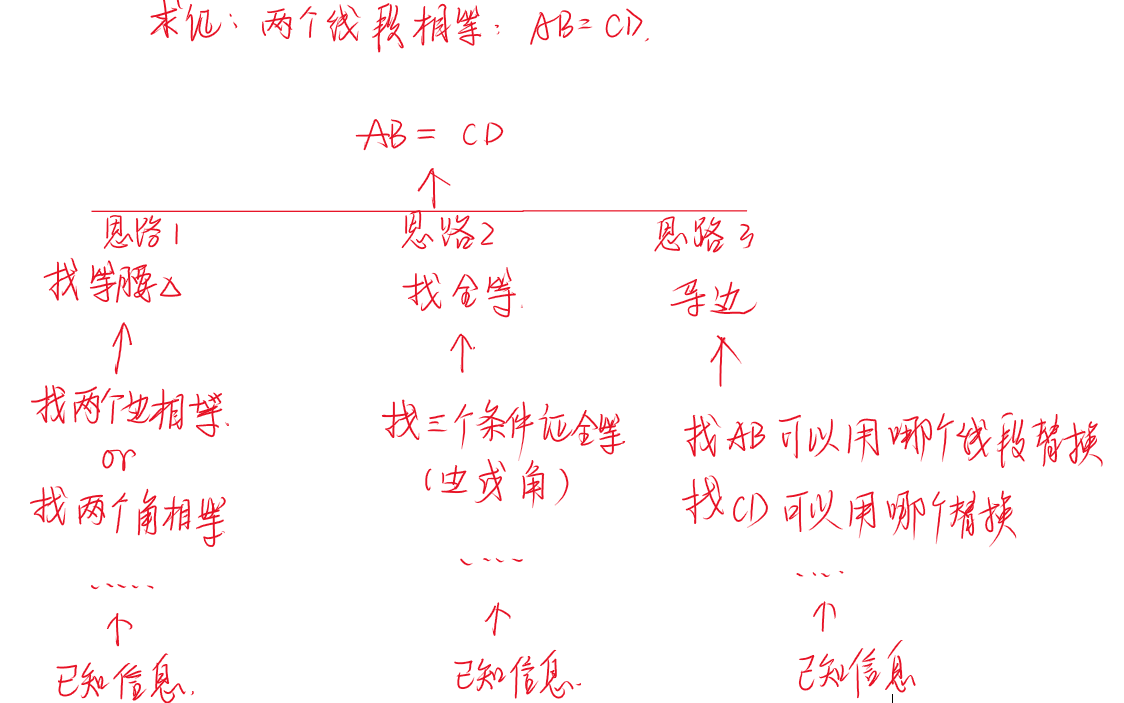
如此一步一步,直到推导到已知信息,那么这个拆解的游戏就完毕了,从上往下是我们反推的逻辑分析过程,从下往上就是证明的书写过程。
📝 写在最后:
几何不是靠“灵感”或“天赋”来解题的,而是靠一个标注—推导—拆解—重组的系统思维过程。只要把这个过程变成习惯,几何题就会越做越顺、越来越有乐趣。
更重要的是,帮他建立一个清晰、可重复的几何解题流程,能真正提升对这门学科的信心和掌控感。
所以,如果你家孩子最近几何学得吃力,别急别慌——这是每个孩子都要经历的“适应期”。
🌱 有了方法,就有了突破。
⬇️ 附一篇旧文,可以参考。
- Author:赵老师
- URL:https://zhaolaoshi.fun/article/1ebd7c25-7723-8022-be66-e00a5bc9c810
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!











